随着制造业系统复杂性、综合性和智能化程度不断提高, 故障预测与健康管理(prognostics and health management, PHM)技术成为解决大型复杂装备关键部件动态维护的最佳选择[1]. 故障预测是PHM的重要组成部分, 可根据状态监测信息中观察到的历史数据和退化趋势来预测部件或系统的剩余使用寿命(remaining useful life, RUL)和故障概率[2]. 故障预测在状态监测、健康状态评估、维护决策间起到重要衔接作用, 对于制造业智能化和数字化发展具有重要的应用价值.
国内外学者们从20世纪90年代开始关注和研究故障预测的相关内容、技术和应用. ISO 13381-1给出了故障预测的定义: 对一个或多个现有和未来故障模式、故障时间和风险的估计. 相对于故障诊断, 故障预测则是预测尚未发生的损害, 包括对剩余寿命的预测和置信度的估计[3]. 根据运行状态数据自动识别健康状态, 进行剩余寿命预测并给出置信度, 是开展视情维修(condition based maintenance, CBM)的重要基础[4].
随着互联网技术和物联网(IoT)的飞速发展, 采集到的数据量呈爆炸式增长, 表现出大容量、低值密度、多源异构、监控数据流等特征, 如何有效处理大量实时数据成为在线故障预测的关键[5]. 此外, 存在数据类不平衡问题, 即正常退化数据较多、故障数据较少, 导致模型偏向性显著[6]. 另一方面, 工程应用较复杂, 故障预测影响因素较多, 数据噪音较大, 在线剩余寿命预测难度较大. 迁移学习为解决上述难点提供了新思路, 其从一个或者多个源领域任务中提取有用知识并将其用在新的目标任务上, 本质是知识的迁移再利用[7]. 极端地, 采集的数据不存在目标故障的数据, 这极大地限制了常规数据驱动方法的应用, 但该情形在工业领域较常见, 如何实现零样本数据情形下的故障诊断与预测成为关注点, 零次学习利用属性迁移方法来解决上述困境[8].
相比于故障诊断, 故障预测的研究较少且综述多停留在2018年前, 对近年来迅猛发展的深度学习、迁移学习和数字孪生技术的涵盖度不高. 考虑到故障预测技术主要集中在剩余寿命预测方面, 对于预测置信度和不确定性综述略显不足. 此外, 缺乏对集成学习、多任务学习、迁移学习、终身学习等学习迁移模式的展望. 为此, 本文通过文献计量法, 运用CiteSpace软件厘清故障预测理论发展脉络, 把握故障预测前沿知识结构, 探明故障预测发展热点迁徙路径并对未来发展趋势进行展望.
1 故障预测知识结构和关联内容分析 1.1 文献数据采集CiteSpace是利用领域内学者们在论文中对文献的选择来鉴别该文献潜力, 其设计理念源于社会网络理论的结构洞方法, 关键节点衡量则是运用了探测频率突增的Burst算法, 整体结构全局性度量选用网络的模块化分析方法[9]. 首先采集特定文献数据, 国内文献部分, 将“故障预测”作为关键词, 对数据进行预处理后得到651篇有效论文数据; 国外文献部分, 分别以“Prognostics”“Fault Prediction”和“Residual Life Prediction”在Web of Science核心库检索, 得到1228篇有效论文数据.
1.2 故障预测知识结构类群提炼通过共被引关系可构建文献知识图谱, 本文运用CiteSpace提炼关键词的知识结构类群. 过滤重复和无效类别后, 国内文献提取得到8个类群, 包括故障诊断、故障预测、gm(1, 1)、PHM、模糊综合评价、bp神经网络、lstm和航天器推进; 国外文献提取得到13个类群, 包括燃气轮机、预测、退化评估、预知性维护、特征学习、振动、故障预测、高压、无损检测、频率解调、电能质量和剩余寿命评估. 除故障预测这一检索关键词, 状态监测、故障诊断、维护决策等PHM主要内容是关联重点; 频率解调、特征学习、退化评估和剩余寿命预测是故障预测的核心内容; 灰色理论、模糊系统和神经网络是故障预测关键技术; 燃气轮机、航天器等机械设备是故障预测主要面向对象. 结合知识结构类群提炼结果, 本文简述故障预测关联内容, 剖析故障预测关键技术, 明晰故障预测研究热点的迁徙过程, 并讨论故障预测发展面临的挑战和未来的发展趋势.
1.3 故障预测关联内容学者们对于故障预测的概念表述上有所差异但核心内涵一致: 在部件或系统仍能正常工作的情况下, 通过设备当前状态以及历史数据来估计部件或系统的剩余寿命, 并预测未来故障发生的可能性[10]. 故障预测是PHM的核心内容, 与状态监测、故障诊断和健康管理存在较强的耦合关联性: 基于状态监测数据进行特征提取, 构建健康指数(health index, HI)进行故障预测, 以此为基础进行维修决策[11]. 其中, 状态监测是通过对一个或多个变量的实时监测来判断系统当前的运行状态, 为故障预测提供系统运行状态的基础信息和数据. 健康管理则是基于故障预测结果、可用资源和使用要求制定维修策略的能力, 涵盖维修替换和备件管理[12]. 上述内容耦合存在两个缺点: 一是特征提取依靠人工经验来提取敏感特征, 泛化能力较弱且会产生较大的人工成本; 二是传统机器学习模型的自学习和泛化能力不能有效应对大数据情形下的健康状态评估和剩余寿命预测[13]. 因此, 深度学习凭借其自动特征提取能力实现端到端的高效故障预测, 从而开展预测性维护决策, 已经成为领域内的研究热点[14].
2 故障预测关键技术本文回顾了常见的故障预测技术分类方法、分类标准和命名规则, 基于故障预测技术含义和覆盖范围, 将其分为以下5类: 基于模型驱动的方法、基于知识驱动的方法、基于统计驱动的方法、基于概率推理的方法和基于数据驱动的方法, 见图 1.

|
图 1 故障预测方法分类 |
基于模型驱动的故障预测方法需要通过建立数学模型来描述机械的退化过程, 包括物理模型和数学模型[15]. 物理模型要明晰运行部件或系统的故障模式及其过程, 通过部件运行状态和工作机理来建立物理模型和随机过程模型, 评估部件和系统性能退化状态并预测剩余寿命[16].经典的物理退化模型包括疲劳裂纹扩展模型、疲劳剥落扩展模型和刚度损伤规律模型等[17]. 其中, 疲劳裂纹扩展模型应用最为广泛, 优势是可以建立影响因素和疲劳寿命的直接联系[18].运用物理模型预测剩余寿命需要构建预测对象的稳态或瞬态负载、温度等信息框架, 结合历史运行情况进行状态预测, 采用数学方法估计参数[19]. 在完全了解故障机理并有效估计模型参数的情形下, 采用模型驱动方法可得到精度较高的剩余寿命预测值.但是, 对于某些复杂机械系统, 由于其内部材质差异和外部故障环境复杂多变, 且系统内模块互为影响, 精准的退化模型难以获得, 无法建立对应的数学模型, 导致预测精度不高.
2.2 基于知识驱动的故障预测技术知识驱动的故障预测技术是通过观测和评估设备运行过程来判断故障类型、推导剩余寿命, 对专家知识依赖性较强, 主要包括专家系统和模糊系统两类[3]. 专家系统利用专家级诊断知识和演绎推理过程判断故障模式和寿命分布, 通过匹配故障规则来提高故障预测精度[20]. 作为专家系统的核心, 推理引擎存在多种形式, 包括规则、模糊逻辑、神经网络和案例等, 已被用于液压系统、滚动轴承和离心泵等设备的故障诊断与预测[21]. 随着故障复杂度增加, 推理机与模糊集、粗糙集、神经网络和案例相融合成连接主义专家系统[22]. 模糊系统利用模糊集对专家知识进行模糊推理, 在不确定环境下进行故障预测. 当下, 模糊系统呈现出了两阶段、自适应和神经网络的拓展, 聚类方法、模糊规则和结构参数均得到优化. 两阶段模糊推理系统、Mamdani模糊推理系统、自适应神经模糊推理系统被提出并应用于刀具、空气压缩机、电容器的剩余寿命预测[23-25]. 模糊系统同时具备专家知识和智能优化的优势, 但需要大量高质量数据进行前期建模.
2.3 基于统计驱动的故障预测技术 2.3.1 回归模型统计驱动的故障预测方法是从历史退化数据的统计特征出发, 通过统计数据建立概率密度函数, 并给出预测结果的置信区间. 其中, 回归分析法技术比较成熟, 可拟合得到自变量与因变量间的关系式, 优化模型参数并做出预测. 多元logistic回归和小波包变换被用于滚动轴承故障诊断, 其性能要优于ANN和SVM[26]. 为提高回归模型拟合精度, 回归分析法与多种理论融合形成了负二项式回归、零膨胀泊松回归、贝叶斯可加回归树、决策树回归等方法, 呈现鲁棒性增加、误差率降低的趋势[27-28].
2.3.2 AR模型及其拓展模型AR模型利用数据相关性建立线性函数进行剩余寿命预测[3]. 针对退化的非线性特征, AR模型改进为退化自回归模型(ND-AR), 结合粒子群算法可实现电池容量退化的多步预测[29]. ARMA模型可应用于轴承的退化状态建模, 将ARMA模型与图神经网络(GNN)联合应用可提高预测准确性[30]. ARIMA模型适用于非平稳数据, 能有效识别退化状态并预测故障, 与XGBoost模型结合、使用小波重构能有效提升预测性能, 可有效评估发动机退化状态[31]. AR模型及其扩展模型的参数识别相对简单、计算复杂度低、预测性能良好, 但依赖于历史观测的趋势信息, 随着时序变长会降低预测准确性.
2.3.3 灰色模型作为时间序列预测的典型方法之一, 灰色模型(gray model, GM)可以将时间序列转化为微分方程, 建立抽象系统的动态发展模型, 仅需要有限的数据来估计未知系统的行为[32]. 因此, 灰色模型适用于小数据和不良信息问题, 通过实时调整系统参数能有效处理噪声和信息缺失情形[33]. GM
比例风险模型(proportional hazards models, PH模型)假设系统的风险率由基线风险函数和协变量函数构成[37]. 通过研究系统寿命周期与相关协变量的关联效应, 确定各参数对系统风险的影响程度, 可用以预测对象RUL[38]. PH模型已被用于航空发动机、轴承、电缆、变速油箱以及制造系统的剩余寿命预测, 并作为视情维修的基础, 体现了实用价值[39].同时, PH模型通过与SVM、径向基函数的组合应用, 能够实现对机械设备退化状态识别和剩余寿命预测[40]. Firth惩罚方法对于提高PH预测准确性、消除过拟合问题有较好性能[41]. 当具备历史数据和监测数据时, PH模型预测精准性较高, 存在数据缺失时需随机过程模型作为协变量函数, 这会加大计算难度并影响预测精准性.
2.4 基于概率推理方法的故障预测技术 2.4.1 分布模型概率推理方法是指从系统的结构及部件的寿命分布等相关信息出发, 通过推断可靠性数量指标探讨系统的最优设计、维护策略等[42]. 概率模型是可靠性数学的核心, 包括常见的寿命分布模型、贝叶斯方法、隐马尔可夫以及随机过程模型. 常见的寿命分布可分为连续型寿命分布、离散型寿命分布和多维寿命分布. 威布尔分布(Weibull distribution, WD)是典型分布之一, 具有形状参数、比例参数以及位置参数.WD可以较好地反映机械产品及其零件在随机载荷下的疲劳强度和疲劳寿命, 由于特征拟合效度不高, 需通过改进故障率函数来提高时域特征拟合效度[43].
2.4.2 贝叶斯方法朴素贝叶斯分类器假设数据集属性之间是相互独立的, 能够分析环境条件对退化趋势影响并进行预测, 有较好的稳健性和预测性能. 朴素贝叶斯条件独立性太强但模型简单, 可以有效防止过拟合, 在锂电池和轴承、刀具等对象上取得了较好的预测性能[44].非朴素贝叶斯分类器则忽略了特征之间独立性的假设, 可采用联合概率分布函数代替边际概率分布来计算概率, 对汽车变速箱、轴承等对象的故障预测具有良好性能[45]. 贝叶斯网络则是一种基于概率的不确定性推理网络, 可用于分析系统故障原因、识别故障模式、预测剩余寿命, 并优化与改进系统设计[46].
2.4.3 HMM模型及其扩展模型隐马尔可夫模型(hidden Markov model, HMM)是一种含有因变量的马尔可夫过程. 离散的HMM和隐半马尔可夫模型(HSMM)在故障模式诊断和故障程度判断中发挥重要作用; 带时间概率的连续HMM和HSMM方法则多用于故障预测[47]. 对于复杂设备, 具有时间结构的HSMM在广义上拓展了马尔可夫假设, 能够对隐藏状态的持续时间建模[48]. HMM模型和粒子群算法、LSTM神经网络的结合使用能有效提升预测性能, 增强模型的可解释性[49]. 针对不可观测的健康状态和复杂动态转换的系统问题, 高阶隐半马尔可夫模型(HOHSMM)的预测框架被提出, 并在涡轮发动机上验证预测性能[50]. HMM模型及扩展模型适用于处理多阶段退化过程, 但由于假设与实际情况不一致, 并且转换概率需要通过大量数据训练得到, 存在较大的获取难度.
2.4.4 随机过程模型随机过程模型可描述退化轨迹, 得到概率框架下的剩余寿命分布, 主要包括Markov链、Gamma过程、逆高斯过程和Wiener过程等方法[51]. Wiener过程应用最为广泛, 其改进包括: 1)将具有恒定阈值的非线性漂移系数的扩散过程转换为具有可变阈值的线性模型[52]; 2)使用递归滤波器来更新维纳过程中的漂移系数[53]; 3)带有自适应漂移和扩散优化[54], 从而实现高精度RUL预测. Wiener过程对非单调过程建模非常有效, 但存在状态依赖导致很难导出RUL的PDF解. 与Wiener过程相似, Gamma过程能够有效描述寿命退化过程, 但受限于马尔可夫假设, 噪声必须服从Gamma分布且对单调过程有效[55]. 逆高斯过程模型(IG)假设机械的退化过程遵循IG分布, 具有独立的增量, 可以有效纳入各种随机效应, 但仍受限于马尔可夫基本假设和单调过程[56].
2.4.5 滤波器方法基于滤波器的故障预测方法包括卡尔曼滤波器和粒子滤波器等, 是一种以综合性和鲁棒性著称的滤波技术[57]. 粒子过滤器属于非线性高斯状态空间模型的蒙特卡洛方法, 能够消减过程的随机性和噪声影响, 实现实时RUL估计, 并且允许多源数据进行逻辑融合[58]. 粒子滤波可用于调整模型参数, 并跟踪非高斯非线性的电池退化过程, 对样本需求量少, 计算速度和效率较高, 但粒子滤波器未能考虑模型不确定性对RUL预测影响[59]. 与粒子滤波不同, 卡尔曼滤波是建立在状态递归和校正模型下, 要求后验是高斯分布, 对故障没有协变量数据的要求[57].
2.5 基于机器学习的故障预测技术 2.5.1 决策树及随机森林决策树是一种以树结构形式表达预测分析过程的模型, 与梯度提升决策树(GBDT)结合可提高预测性能及鲁棒性[60]. 以C4.5算法为核心的决策树已对轴承、齿轮、离心泵等机械设备实现故障诊断和故障预测[61]. 为进一步提高预测性能, 降低过拟合风险, 随机森林算法(random forest, RF)应运而生, 其对电池以及刀具等对象的预测性能较高. RF模型通过改进模型得到增强型随机森林算法, 能够降低模型的复杂性, 提高故障诊断模型的准确性和可解释性[62]. 运用粒子群能优化随机森林参数也可以提高预测精准性, 已经在滚动轴承上得以验证[63].
2.5.2 支持向量机支持向量机(SVM)与相关向量机(RVM)的原理都是基于核函数映射将低维空间非线性问题转化为高维空间的线性问题. 不同地, RVM是基于贝叶斯框架, 先验参数通过主动相关决策理论来稀疏模型, 训练速度快且具备良好的泛化能力[64]. 为了提高SVM预测精准性, 一方面, 拓展模型, 得到最小二乘SVM、近似SVM、小波SVM、模糊SVM和集成SVM; 另一方面, 通过粒子群优化SVM内核参数, 优势是不需要历史运行状态信息, 其性能在飞机发动机上得以验证[65]. 对于RVM性能优化, 卡尔曼滤波器通过动态调整系数矩阵和相关向量, 可以提高航空器电池RUL预测性能[66].
2.5.3 人工神经网络BP神经网络是多层前馈神经网络, 具有非线性映射能力和柔性网络结构. 基于多层感知器(MLP)的人工神经网络(ANN)则具有自学习、自组织的优势, 拥有较强的非线性函数逼近能力, 在故障预测中应用较为广泛, 主要面向滚动轴承、齿轮、马达、电动机、发动机等机械设备[67]. 对于ANN的改进包括径向基函数神经网络(RBFNN)、小波神经网络(WNN)和贝叶斯正则径向基函数神经网络(trainbr-RBFNN)等, 剩余寿命预测性能较好[68]. 值得一提的是, 深度学习赋予神经网络新的生命力, 深度神经网络已经成为故障预测的前沿技术.
2.6 基于深度学习的故障预测技术 2.6.1 自编码器自编码器(autoencoder, AE)通过对输入信息进行表征学习来实现异常监测、数据去噪和特征降维, 并且输出可作为后续学习模型的输入[69]. AE由编码和解码两部分组成, 参照文献[21]对原理进行简述.给定数据集:
| $ \begin{align} {{\mathit{\boldsymbol{h}}}_i} = {f_\theta }({{\mathit{\boldsymbol{x}}}_i}) = {\sigma _f}({{\mathit{\boldsymbol{\omega}}}^{{\rm T}} } \cdot {{\mathit{\boldsymbol{x}}}_i} + {\mathit{\boldsymbol{b}}}). \end{align} $ | (1) |
其中:
| $ \begin{align} {{\mathit{\boldsymbol{\hat x}}}_i} = {g_{\theta '}}({{\mathit{\boldsymbol{h}}}_i}) = {\sigma _g}({{\mathit{\boldsymbol{\omega}} '}^{{\rm T}} } \cdot {{\mathit{\boldsymbol{h}}}_i} + {\mathit{\boldsymbol{b}}'}). \end{align} $ | (2) |
| $ \begin{align} \mathop {\min }\limits_{\theta , \theta '} \;L( {{{\mathit{\boldsymbol{x}}}_i}, {{{\mathit{\boldsymbol{\hat x}}}}_i}}) = \frac{1}{{2m}}{ \sum\limits_{i = 1}^m {\| {{{\mathit{\boldsymbol{x}}}_i} - {{{\mathit{\boldsymbol{\hat x}}}}_i}} \|} ^2}. \end{align} $ | (3) |
AE的拓展模型包括堆叠AE、稀疏AE、变分AE、收缩AE和卷积AE等, 在故障预测中取得了较高精准性[21]. 此外, 自编码器可与递归神经网络、卷积神经网络等方法进行联合预测, 现已实现系统级的剩余寿命预测[70]. AE及其扩展模型不依赖专家知识, 属于无监督学习, 但无法直接识别健康状态并预测RUL, 因此在训练过程中需要带标签样本.
2.6.2 卷积神经网络作为应用最广泛的深度学习算法之一, 卷积神经网络(convolutional neural networks, CNN)的表征学习能力可以提取高阶特征, 已被应用于轴承、电子等设备故障预测中, 具有较高的预测精度和鲁棒性[71]. CNN通常由卷积层、池化层和全连接层组成.卷积层特征映射原理简述如下:
三维卷积核对
| $ \begin{align} {{\mathit{\boldsymbol{Y}}}^p} = &f({{\mathit{\boldsymbol{Z}}}^p}) = {{\mathit{\boldsymbol{W}}}^p} \otimes {\mathit{\boldsymbol{X}}} + {{\mathit{\boldsymbol{b}}}}^p = \\ & \sum\limits_{d = 1}^D {{{\mathit{\boldsymbol{W}}}^{p, d}} \otimes } {{\mathit{\boldsymbol{X}}}^d} + {{{\mathit{\boldsymbol{b}}}}^p}. \end{align} $ | (4) |
基于CNN的体系结构, 可分为二维(2D)CNN、一维(1D)CNN两类. 考虑到机械故障预测输入数据通常为一维信号数据, 无法直接进行2DCNN处理, 学者们分别从以下3个方面着手: 一是信号处理, 包括小波变换、双树复数小波变换、同步压缩变换等[72]; 二是重构矩阵, 通过调整输入矩阵尺寸使其适用于CNN模型, 降低了对专家知识的依赖[73]; 三是图像数据, 通过灰度图像和红外图像可直接输入图片进行2DCNN建模预测[74], 现已实现滚动轴承、齿轮、马达和液压泵等对象的故障预测. 基于CNN的故障预测模型能够直接从状态监测数据中学习到表征特征, 无需进行数据滤波、转换等预处理. 此外, CNN能够通过共享权重来减少训练参数数量, 虽然能够加速收敛并抑制过度拟合, 但需要大量的标记样本.
2.6.3 循环神经网络循环神经网络(recurrent neural network, RNN)是一类具有短期记忆能力的神经网络, 适合处理时间序列数据. RNN的神经元可以同时接受来自自身和其他神经元的信息, 形成具有环路的网络结构, 这导致网络存在长期依赖问题. 为此, 引入门控机制来控制信息的累积速度, 主要包括长短期记忆网络(long short-term memory, LSTM)和门控循环单元网络(gated recurrent unit, GRU)[75], 本文选择LSTM进行原理简述.
1) 长短期记忆网络(LSTM). LSTM是RNN的一个变体, 可以有效地解决梯度爆炸或消失问题, 并且通过引入时间概念的步长边缘来增强学习, 流程见图 2[76].
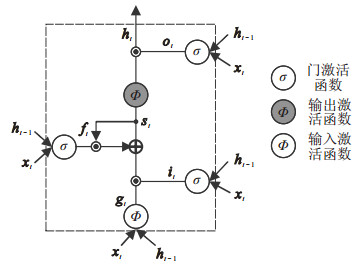
|
图 2 LSTM模型示意图 |
基本理论如下: 在
| $ \begin{align} \begin{cases} {{\mathit{\boldsymbol{h}}}_t} = f({{\mathit{\boldsymbol{w}}}_{hx}}{{\mathit{\boldsymbol{x}}}_t} + {{\mathit{\boldsymbol{w}}}_{hh}}{{\mathit{\boldsymbol{h}}}_{t - 1}} + {{\mathit{\boldsymbol{b}}}_h}), \\[-5pt] {{{\mathit{\boldsymbol{\hat y}}}}_t} = f({{\mathit{\boldsymbol{w}}}_{yx}}{{\mathit{\boldsymbol{h}}}_t} + {{\mathit{\boldsymbol{b}}}_y}). \end{cases} \end{align} $ | (5) |
其中:
在故障预测中, LSTM模型呈现3个方向上的改进, 一是与CNN模型、Elman神经网络和RNN模型等进行联合应用, 能有效提升剩余寿命预测性能[77]; 二是LSTM改进模型, 如AST-LSTM NN模型, 通过设计增强型LSTM细胞结构使改进LSTM模型具有主动跟踪单元状态的功能, 从而实现准确且稳健的多步剩余寿命预测[78]; 三是构建卷积LSTM模型(CLSTM), 相对于CNN和LSTM模型, 其具有更好的准确性和计算效率[79]. 尽管LSTM及其扩展模型可以消除部分梯度消失问题, 但训练路径较为复杂, 计算费时, 且对计算机硬件要求较高.
2) 门控循环单元网络(GRU). 相对于LTSM, GRU引入一个更新门来控制当前状态需要保留的信息, 以及需接受的新信息[80]. 随着现代工业发展, 机器健康监控系统(MHMS)已得到广泛应用, 其目标是实现预测性维护. GRU、双向GRU网络发展实现了对工具、齿轮箱和轴承的健康评估和故障预测, 为主动维护提供了重要保障[81]. 相比于LSTM, GRU的模型参数更少, 计算速度更快, 但对于长期依赖关系的处理不如LSTM.
2.6.4 深度信念网络深度信念网络(deep belief network, DBN)基于受限玻尔兹曼机实现了逐层训练, 为整个网络赋予了较好的初始权值, 有效解决了深层次神经网络的优化问题[82], 其原理简述如下: 对于一个有
| $ \begin{align} p( {{{{\mathit{\boldsymbol{h}}}^{( l )}}}|{{\mathit{\boldsymbol{h}}}^{( {l + 1} )}}, \ldots, {{\mathit{\boldsymbol{h}}}^{( L )}}} ) = p( {{{{\mathit{\boldsymbol{h}}}^{( l)}}}|{{\mathit{\boldsymbol{h}}}^{( {l + 1} )}}}). \end{align} $ | (6) |
深度信念网络中所有变量的联合概率可分解为
| $ \begin{align} &p( {{\mathit{\boldsymbol{v}}}, {{\mathit{\boldsymbol{h}}}^{( 1)}}, \ldots, {{\mathit{\boldsymbol{h}}}^{( L )}}} ) = \\[-3pt] &\Big( { \prod\limits_{l = 0}^{L - 1} {p( {{{{\mathit{\boldsymbol{h}}}^{( l )}}} |{{\mathit{\boldsymbol{h}}}^{( {l + 1} )}}})} }\Big)p( {{{\mathit{\boldsymbol{h}}}^{( {L - 1} )}}, {{\mathit{\boldsymbol{h}}}^{( L )}}} ). \end{align} $ | (7) |
其中
| $ \begin{align} p( {{{{\mathit{\boldsymbol{h}}}^{( l)}}}|{{\mathit{\boldsymbol{h}}}^{( {l + 1})}}} ) = \sigma ( {{{\mathit{\boldsymbol{a}}}^{( l )}}+{{\mathit{\boldsymbol{W}}}^{( {l + 1})}}{{\mathit{\boldsymbol{h}}}^{( {l + 1})}}}). \end{align} $ | (8) |
其中:
DBN可用于检测机械设备的故障, 准确率要优于ANN和SVM[83]. 深度信念网络可以通过逐层训练和精调解决梯度消失问题并给出较好的初始参数, 从而达到优化深度神经网络的目的. 由于DBN理论基础是概率图模型, 模型具有较好的可解释性, 但计算成本较高, 并且基于最大似然训练近似值去优化网络的步骤尚不清楚, 尚无法解决输入图像的二维结构[84]. 因此, 相比于其他深度学习模型在故障预测中的使用频率较低, 但研究价值较大.
故障预测关键技术分类汇总见表 1.
| 表 1 故障预测关键技术分类汇总表 |
近30年来, 国内外的故障预测研究都经历了快速发展. 本文运用了CiteSpace中的Burst算法确定国内外故障预测研究关键突变节点及辐射区间, 并比对了高倍引论文的研究重点、关键技术和应用现状. 发现: 1993年, 学者开始关注故障预测, 但主要停留在现状阐述; 2000年, 故障预测研究进入活跃期, 研究成果丰硕、引用频次剧增, 内容涵盖PHM主要模块, 机器学习方法应用率大幅提升; 2007年, 传感器技术和人工智能技术提升, 故障预测技术体系化发展, 深度学习方法逐步应用; 2014年, 进入深度学习技术井喷期, 各类方法得以改进, 且组合预测和融合预测成为趋势, 聚焦于方法论研究. 故障预测理论体系、方法体系和技术体系支撑其形成新学科框架, 并着手讨论工程情形下在线预测、迁移学习和跨工况应用模式. 因此, 本文将近30年的发展归纳为以下4个阶段: 理论奠基期(1993年
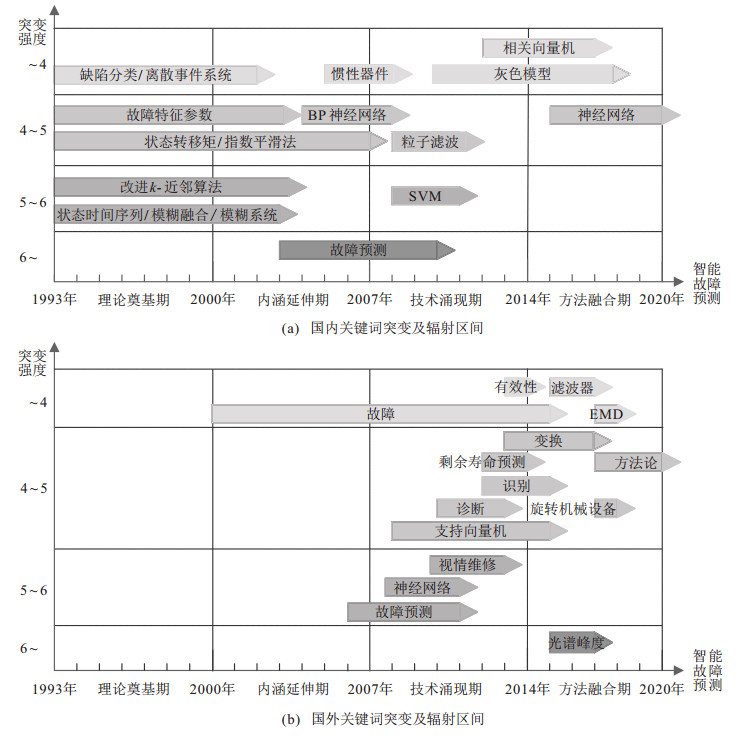
|
图 3 国内外关键词突变及辐射区间 |
这一阶段, 国内外故障预测研究均处于起步阶段, 存在缺乏实时数据以及阈值不确定的问题, 故障预测技术以模型驱动、统计驱动、概率推理等方法为主. 国内学者们讨论了机械设备、火电机组故障的机理、监测、诊断与预测的研究现状、现存问题及发展重点, 分别运用改进灰色理论、马尔可夫、神经网络等方法进行故障预测建模, 实现了空间推进系统、传感器、汽轮机等单部件预测, 对于系统故障模式识别和预测尚处于起步阶段. 国外研究运用实时专家系统、神经网络、概率论和粗糙集算法等方法对模拟电路、复杂电子系统、发动机和航空航天零部件等对象进行故障模式识别和预测, 故障阈值确定和系统建模成为故障预测建模的难点[85]. 分层建模的思路被应用于系统故障模式中, 并实现剩余寿命预测[86].
3.2 故障预测内涵延伸期(2000年这一阶段, 国内外较为关注数据融合、阈值确定、系统预测和不确定问题. 国内学者们运用滤波器自适应预测、模糊综合评判、灰色理论、神经网络方法对机械设备、电力设备和复杂武器装备进行故障预测. 对于阈值确定难点, 小波阈值法在预测机械设备的早期故障取得了良好成效[87]. 有学者提出了一种可修系统的故障统计模型和维修周期预测方法, 开始向预防性维修发展[88]. 国外研究聚焦于人工智能技术, 改进的神经网络模型对解决复杂问题和不确定性问题具有很好的效果, 被广泛应用于机械设备故障预测[89]. 随着多传感器数据的融合技术陆续出现, 解决了系统预测困境[4], 数据级融合、特征级融合和决策级融合是主要发展方向, 多用于磨削刀具、柴油机、电池等对象的状态监测与故障预测, 并以此为基础建立维护维修框架.
3.3 故障预测技术涌现期(2007年随着数据采集技术、信息技术以及人工智能技术的迅速发展, 基于测试数据或传感器数据的数据驱动技术成为了故障预测领域的研究热点, 综合应用方法和融合改进方法也是提高预测性能的有效方法[90]. 国内研究中, 模糊理论、粗糙集理论、灰色理论、证据理论等数学方法为故障预测技术发展奠定了坚实的理论基础[91], 基于KPCA多通道特征信息融合方法受到重视[92]. 以状态为基础、以故障预测为核心的预防性维修方法受到关注, 视情维修成为热点[93]. 国外部分, 自组织图、神经网络、粒子滤波器、支持向量机、遗传算法等机器学习方法被运用于故障预测[94].此外, 小波分解与滤波技术、在线粒子滤波器、高阶粒子滤波技术和递归滤波器[53]被开发用于故障诊断和剩余寿命预测, 并与隐马尔可夫模型(HMM)、蒙特卡罗模拟、维纳过程和自适应神经模糊推理系统等方法相结合, 提高了故障预测的精确性和计算效率.
3.4 故障预测方法融合期(2014年至今)在大数据背景下, 国内外对故障预测相关研究进行综述并提取方法论, 主要集中在工程技术类别. 基于数据驱动的深度学习方法成为解决数据非线性、变量耦合、时序相关、滞后等问题的关键. 在此期间, 国内出现了多篇高被引的综述类文章, 重点论述了不同侧重点下数据驱动故障预测技术[11, 95], 明确了故障预测和健康管理的体系框架, 已经在航空航电、风电机组、机电设备、机械设备、电子系统等领域广泛应用[96]. 国外研究探讨了深度学习在故障预测领域内的体系结构、相关理论和最新趋势[97]. 技术层面, 深度神经网络(DNN)的改进、融合应用取得了较大突破[12]: 递归神经网络(RNN-HI)[76]、深度卷积神经网络(DCNN)[98]、AST-LSTM深度神经网络[78]、卷积LSTM(CLSTM)深度神经网络[79]等模型在剩余寿命预测中取得了更好的准确性和计算效率.
在工程场景中, 迁移学习、零次学习、数字孪生等新模式引入, 解决了复杂工况和数据样本缺失等应用困境. Lei等[21]认为迁移学习有望将智能故障诊断从学术研究扩展到工程方案, 分别提出了基于特征、基于生成对抗网络(GAN)、基于实例和基于参数的迁移学习方法; Shao等[99]提出了一种改进的带迁移学习的卷积神经网络方法, 解决了训练数据受限问题; Feng等[8]提出了零次学习新模式, 利用属性迁移方法来解决零样本故障诊断和预测问题; Booyse等[100]提出以深度数字孪生(DDT)的形式进行在线故障诊断和故障预测, 有助于实现预测性维护决策.
4 结论与展望 4.1 研究结论借助CiteSpace对故障预测的文献数据进行量化分析, 从“文献追踪”的角度挖掘故障预测发展的知识结构、分布脉络和研究热点, 这是对故障预测综述类研究的一个新尝试. 总体而言, 故障预测技术发展多元化趋势显著, 与实践背景锲合度逐步提高, 被广泛应用于航空航电、风电机组、机电设备、机械设备、电子系统等领域. 现阶段, 基于深度学习的故障预测技术成为发展热点, 状态监测、阈值优化、多源融合(数据级融合、特征级融合和决策级融合)、不确定性评估仍是提高预测精准性的核心.
从知识结构来看, 故障预测与状态监测、故障诊断和健康管理组成了PHM核心系统, 板块间存在较强的耦合关联性. 故障预测关键技术发展方向丰富, 可以分为基于模型驱动的方法、基于知识驱动的方法、基于统计驱动的方法、基于概率推理的方法和基于数据驱动(包括机器学习和深度学习)的方法, 提升数据质量、实现在线预测和完善迁移学习成为发展趋势. 现阶段, 基于深度学习的故障预测技术在数据预处理、特征提取和混合集成建模中取得了良好成效, 具有自动特征提取、解决数据不平衡问题和优化模型参数等优势, 预测性能高但算法复杂性也高, 需避免模型退化和过拟合, 对计算机要求较高.
从热点迁徙过程看, 故障预测发展经历了4个阶段: 理论奠基期、内涵延伸期、技术涌现期和方法融合期. 理论奠基期, 数学基础融入到预测理论、统计技术方法占主导, 阈值不确定性和系统预测是难点. 内涵延伸期, 基于状态监测和故障预测的预测性维修策略备受关注, 改进的神经网络模型对解决复杂问题和不确定性问题具有很好的效果. 技术涌现期, 包括灰色理论、模糊理论、粗糙集理论、证据理论、系统仿真理论等数学理论纳入到预测方法, 基于测试数据或传感器数据的数据驱动类故障预测技术成为研究热点, 预测不确定性依旧是难点. 方法融合期, 大数据背景下, 数据驱动成为关键词; 基于数据驱动的深度学习方法成为解决数据非线性、变量耦合、时序相关、滞后等问题的关键; 同时, 迁移学习、零次学习、数字孪生等新模式成为故障预测学术研究扩展到工程方案的有效途径.
4.2 未来展望随着机器学习、深度学习和迁移学习等技术的发展, 智能故障预测能自动识别对象健康状态、预测故障及余寿, 并为将来的工程场景服务提供方法. 本文探明了故障预测发展路线并讨论了智能故障预测的未来挑战, 尝试提出了未来五到十年该领域的潜在发展趋势, 见图 4.
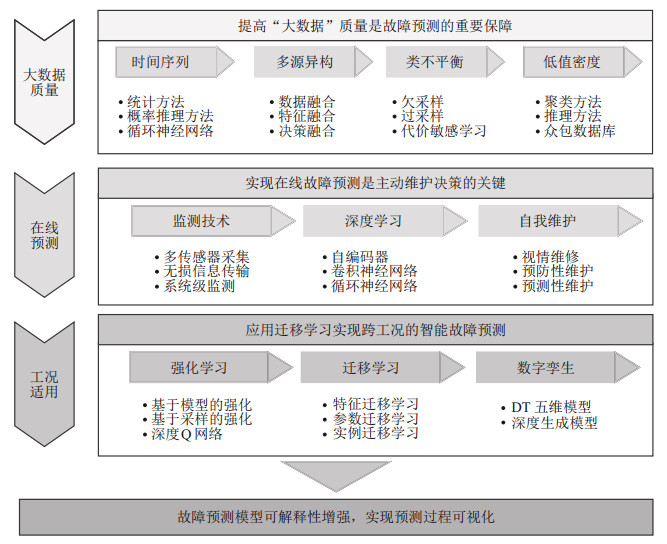
|
图 4 故障预测未来发展趋势 |
1) 提高数据收集质量, 充分考虑时间序列数据可能存在不平稳、相关性和长短期依赖问题. 此外, 大数据背景下带来的数据多源异构性、类不平衡问题以及数据低值性也需重视.
2) 实现在线故障预测. 随着传感器技术和物联网技术的发展, 状态监测和实时在线故障预测成为可能. 在监测过程, 需要明确系统级和部件级监测的区别, 在系统配置的众多传感器中找到关键模块传感器, 并实现无损传输尤为重要. 数据传输后进行预处理并进入深度学习模型中, 达到高精度的状态识别和故障预测是实现自主动态维护的重要保障.
3) 跨工况的迁移学习. 深度学习的感知能力和强化学习的决策能力为未来自主决策提供了重要支撑. 其中, 迁移学习为跨工况、跨任务的故障预测提供实现路径, 主要包括特征、示例和参数的迁移学习. 此外, 基于生成对抗网络(GAN)的深度迁移学习为故障预测提供了良好的体系框架, 是未来发展的重要趋势. 数字孪生技术可充分利用物理模型、传感器数据、仿真过程等, 在虚拟空间中完成映射和建模, 在智能制造领域成为讨论热点之一. 深度强化学习、深度迁移学习和深度数字孪生技术为跨工况智能故障预测提供了研究方向和应用热点.
本文系统地介绍了故障预测的知识结构、关键技术和热点迁移过程, 为该领域的未来研究应用提供了有价值的参考.
| [1] |
Lee J, Wu F J, Zhao W Y, et al. Prognostics and health management design for rotary machinery systems — Reviews, methodology and applications[J]. Mechanical Systems and Signal Processing, 2014, 42(1/2): 314-334. |
| [2] |
Lei Y G, Li N P, Guo L, et al. Machinery health prognostics: A systematic review from data acquisition to RUL prediction[J]. Mechanical Systems and Signal Processing, 2018, 104: 799-834. DOI:10.1016/j.ymssp.2017.11.016 |
| [3] |
Sikorska J Z, Hodkiewicz M, Ma L. Prognostic modelling options for remaining useful life estimation by industry[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1803-1836. DOI:10.1016/j.ymssp.2010.11.018 |
| [4] |
Jardine A K S, Lin D M, Banjevic D. A review on machinery diagnostics and prognostics implementing condition-based maintenance[J]. Mechanical Systems and Signal Processing, 2006, 20(7): 1483-1510. DOI:10.1016/j.ymssp.2005.09.012 |
| [5] |
Xu X F, Lei Y G, Li Z D. An incorrect data detection method for big data cleaning of machinery condition monitoring[J]. IEEE Transactions on Industrial Electronics, 2020, 67(3): 2326-2336. DOI:10.1109/TIE.2019.2903774 |
| [6] |
Jia F, Lei Y G, Lu N, et al. Deep normalized convolutional neural network for imbalanced fault classification of machinery and its understanding via visualization[J]. Mechanical Systems and Signal Processing, 2018, 110: 349-367. DOI:10.1016/j.ymssp.2018.03.025 |
| [7] |
Pan S J, Yang Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 22(10): 1345-1359. |
| [8] |
Feng L J, Zhao C H. Fault description based attribute transfer for zero-sample industrial fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2021, 17(3): 1852-1862. DOI:10.1109/TII.2020.2988208 |
| [9] |
Chen C M. Predictive effects of structural variation on citation counts[J]. Journal of the American Society for Information Science and Technology, 2012, 63(3): 431-449. DOI:10.1002/asi.21694 |
| [10] |
Engel S J, Gilmartin B J, Bongort K, et al. Prognostics, the real issues involved with predicting life remaining[C]. 2000 IEEE Aerospace Conference Proceedings. Big Sky: IEEE, 2000: 457-469.
|
| [11] |
彭宇, 刘大同. 数据驱动故障预测和健康管理综述[J]. 仪器仪表学报, 2014, 35(3): 481-495. (Peng Y, Liu D T. Data-driven prognostics and health management: A review of recent advances[J]. Chinese Journal of Scientific Instrument, 2014, 35(3): 481-495.) |
| [12] |
Jia F, Lei Y G, Lin J, et al. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data[J]. Mechanical Systems and Signal Processing, 2016, 72(72/73): 303-315. |
| [13] |
Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [14] |
Pecht M G, Joai R. A prognostics and health management roadmap for information and electronics-rich systems[J]. IEICE ESS Fundamentals Review, 2010, 3(4): 425-432. |
| [15] |
Vichare N M, Pecht M G. Prognostics and health management of electronics[J]. IEEE Transactions on Components and Packaging Technologies, 2006, 29(1): 222-229. DOI:10.1109/TCAPT.2006.870387 |
| [16] |
Di Y, Jin C, Bagheri B, et al. Fault prediction of power electronics modules and systems under complex working conditions[J]. Computers in Industry, 2018, 97: 1-9. DOI:10.1016/j.compind.2018.01.011 |
| [17] |
Lu Y Z, Christou A. Prognostics of IGBT modules based on the approach of particle filtering[J]. Microelectronics Reliability, 2019, 92: 96-105. DOI:10.1016/j.microrel.2018.11.012 |
| [18] |
Lei Y G, Li N P, Gontarz S, et al. A model-based method for remaining useful life prediction of machinery[J]. IEEE Transactions on Reliability, 2016, 65(3): 1314-1326. DOI:10.1109/TR.2016.2570568 |
| [19] |
Tinga T, Loendersloot R. Predictive maintenance in dynamic systems: Advanced methods, decision support tools and real-world applications[M]. Berlin: Springer, 2019: 313-353.
|
| [20] |
Husain Z. Fuzzy logic expert system for incipient fault diagnosis of power transformers[J]. International Journal on Electrical Engineering and Informatics, 2018, 10(2): 300-317. DOI:10.15676/ijeei.2018.10.2.8 |
| [21] |
Lei Y G, Yang B, Jiang X W, et al. Applications of machine learning to machine fault diagnosis: A review and roadmap[J]. Mechanical Systems and Signal Processing, 2020, 138: 106587. |
| [22] |
Sahin S, Tolun M R, Hassanpour R. Hybrid expert systems: A survey of current approaches and applications[J]. Expert Systems with Applications, 2012, 39(4): 4609-4617. DOI:10.1016/j.eswa.2011.08.130 |
| [23] |
Aliustaoglu C, Ertunc H M, Ocak H. Tool wear condition monitoring using a sensor fusion model based on fuzzy inference system[J]. Mechanical Systems and Signal Processing, 2009, 23(2): 539-546. DOI:10.1016/j.ymssp.2008.02.010 |
| [24] |
Sharma A K, Singh V, Verma N K, et al. Condition based monitoring of machine using Mamdani fuzzy network[C]. 2018 Prognostics and System Health Management Conference. Chongqing: IEEE, 2018: 1159-1163.
|
| [25] |
Jamshidi M B, Alibeigi N. Neuro-fuzzy system identification for remaining useful life of electrolytic capacitors[C]. 2017 International Conference on System Reliability and Safety(ICSRS). Milan: IEEE, 2017: 227-231.
|
| [26] |
Pandya D H, Upadhyay S H, Harsha S P. Fault diagnosis of rolling element bearing by using multinomial logistic regression and wavelet packet transform[J]. Soft Computing, 2014, 18(2): 255-266. DOI:10.1007/s00500-013-1055-1 |
| [27] |
Weyuker E J, Ostrand T J, Bell R M. Comparing the effectiveness of several modeling methods for fault prediction[J]. Empirical Software Engineering, 2010, 15(3): 277-295. DOI:10.1007/s10664-009-9111-2 |
| [28] |
Rathore S S, Kumar S. An empirical study of some software fault prediction techniques for the number of faults prediction[J]. Soft Computing, 2017, 21(24): 7417-7434. DOI:10.1007/s00500-016-2284-x |
| [29] |
Liu D T, Luo Y, Liu J, et al. Lithium-ion battery remaining useful life estimation based on fusion nonlinear degradation AR model and RPF algorithm[J]. Neural Computing and Applications, 2014, 25(3/4): 557-572. |
| [30] |
Wang H W, Xiao G Y, Han N, et al. Session-based graph convolutional ARMA filter recommendation model[J]. IEEE Access, 2020, 8: 62053-62064. DOI:10.1109/ACCESS.2020.2984039 |
| [31] |
Wang Y, Guo Y K. Forecasting method of stock market volatility in time series data based on mixed model of ARIMA and XGBoost[J]. China Communications, 2020, 17(3): 205-221. DOI:10.23919/JCC.2020.03.017 |
| [32] |
Deng J L. Control problems of grey systems[J]. Systems & Control Letters, 1982, 1(5): 288-294. |
| [33] |
Kayacan E, Ulutas B, Kaynak O. Grey system theory-based models in time series prediction[J]. Expert Systems with Applications, 2010, 37(2): 1784-1789. DOI:10.1016/j.eswa.2009.07.064 |
| [34] |
Zeng B, Duan H M, Zhou Y F. A new multivariable grey prediction model with structure compatibility[J]. Applied Mathematical Modelling, 2019, 75: 385-397. DOI:10.1016/j.apm.2019.05.044 |
| [35] |
Dejamkhooy A, Dastfan A, Ahmadyfard A. Modeling and forecasting nonstationary voltage fluctuation based on grey system theory[J]. IEEE Transactions on Power Delivery, 2017, 32(3): 1212-1219. DOI:10.1109/TPWRD.2014.2386696 |
| [36] |
黄魁, 苏春. 基于灰色神经网络组合模型的故障预测[J]. 系统工程与电子技术, 2020, 42(1): 238-244. (Huang K, Su C. Fault prediction based on combination model of grey neural network[J]. Systems Engineering and Electronics, 2020, 42(1): 238-244.) |
| [37] |
Cox D R. Regression models and life‐tables[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1972, 34(2): 187-202. DOI:10.1111/j.2517-6161.1972.tb00899.x |
| [38] |
Banjevic D, Jardine A K S. Calculation of reliability function and remaining useful life for a Markov failure time process[J]. IMA Journal of Management mathematics, 2006, 17(2): 115-130. DOI:10.1093/imaman/dpi029 |
| [39] |
Wang L, Zhang L, Wang X Z. Reliability estimation and remaining useful lifetime prediction for bearing based on proportional hazard model[J]. Journal of Central South University, 2015, 22(12): 4625-4633. DOI:10.1007/s11771-015-3013-9 |
| [40] |
Veisi M S, Rezaei S, Salehivaysi K. Comparing sensitivity of radial basis function method with multilayer perceptron network and Cox proportional hazard model in survival data[J]. International Journal of Computer Science and Network Security, 2017, 17(7): 180-187. |
| [41] |
Adhikary A C, Shafiqur R M. Firth's penalized method in Cox proportional hazard framework for developing predictive models for sparse or heavily censored survival data[J]. Journal of Statistical Computation and Simulation, 2021, 91(3): 445-463. DOI:10.1080/00949655.2020.1817924 |
| [42] |
曹晋华, 程侃. 可靠性数学引论[M]. 北京: 高等教育出版社, 2006: 2-6. (Cao J H, Cheng K. Introduction to reliability mathematics[M]. Beijing: Higher Education Press, 2006: 2-6.) |
| [43] |
Ali J B, Chebel-Morello B, Saidi L, et al. Accurate bearing remaining useful life prediction based on Weibull distribution and artificial neural network[J]. Mechanical Systems and Signal Processing, 2015, 56/57: 150-172. DOI:10.1016/j.ymssp.2014.10.014 |
| [44] |
Zhang N N, Wu L F, Wang Z H, et al. Bearing remaining useful life prediction based on Naive Bayes and Weibull distributions[J]. Entropy, 2018, 20(12): 944. DOI:10.3390/e20120944 |
| [45] |
Yu J, Ding B, He Y J. Rolling bearing fault diagnosis based on mean multigranulation decision-theoretic rough set and non-naive Bayesian classifier[J]. Journal of Mechanical Science and Technology, 2018, 32(11): 5201-5211. DOI:10.1007/s12206-018-1018-7 |
| [46] |
Mosallam A, Medjaher K, Zerhouni N. Data-driven prognostic method based on Bayesian approaches for direct remaining useful life prediction[J]. Journal of Intelligent Manufacturing, 2016, 27(5): 1037-1048. DOI:10.1007/s10845-014-0933-4 |
| [47] |
Soualhi A, Clerc G, Razik H, et al. Hidden Markov models for the prediction of impending faults[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3271-3281. DOI:10.1109/TIE.2016.2535111 |
| [48] |
Yu S Z. Hidden semi-Markov models[J]. Artificial Intelligence, 2010, 174(2): 215-243. |
| [49] |
Tao Z R, An Q L, Liu G Y, et al. A novel method for tool condition monitoring based on long short-term memory and hidden Markov model hybrid framework in high-speed milling Ti-6Al-4V[J]. The International Journal of Advanced Manufacturing Technology, 2019, 105(7): 3165-3182. |
| [50] |
Liao Y, Xiang Y S, Wang M. Health assessment and prognostics based on higher‐order hidden semi‐Markov models[J]. Naval Research Logistics(NRL), 2021, 68(2): 259-276. DOI:10.1002/nav.21947 |
| [51] |
胡昌华, 施权, 司小胜, 等. 数据驱动的寿命预测和健康管理技术研究进展[J]. 信息与控制, 2017, 46(1): 72-82. (Hu C H, Shi Q, Si X S, et al. Data-driven life prediction and health management: state of the art[J]. Information and Control, 2017, 46(1): 72-82.) |
| [52] |
Si X S, Wang W B, Hu C H, et al. Remaining useful life estimation based on a nonlinear diffusion degradation process[J]. IEEE Transactions on Reliability, 2012, 61(1): 50-67. DOI:10.1109/TR.2011.2182221 |
| [53] |
Si X S, Wang W B, Hu C H, et al. A Wiener-process-based degradation model with a recursive filter algorithm for remaining useful life estimation[J]. Mechanical Systems and Signal Processing, 2013, 35(1/2): 219-237. |
| [54] |
Wang H, Ma X B, Zhao Y. An improved Wiener process model with adaptive drift and diffusion for online remaining useful life prediction[J]. Mechanical Systems and Signal Processing, 2019, 127: 370-387. DOI:10.1016/j.ymssp.2019.03.019 |
| [55] |
Yan H C, Zhou J H, Pang C K. Gamma process with recursive MLE for wear PDF prediction in precognitive maintenance under aperiodic monitoring[J]. Mechatronics, 2015, 31: 68-77. DOI:10.1016/j.mechatronics.2015.05.009 |
| [56] |
Hao S H, Yang J, Berenguer C. Degradation analysis based on an extended inverse Gaussian process model with skew-normal random effects and measurement errors[J]. Reliability Engineering & System Safety, 2019, 189: 261-270. |
| [57] |
Baptista M, Henriques E P, De Medeiros I, et al. Remaining useful life estimation in aeronautics: Combining data-driven and Kalman filtering[J]. Reliability Engineering & System Safety, 2019, 184: 228-239. |
| [58] |
Zio E, Peloni G. Particle filtering prognostic estimation of the remaining useful life of nonlinear components[J]. Reliability Engineering & System Safety, 2011, 96(3): 403-409. |
| [59] |
Xing Y J, Ma E W M, Tsui K L, et al. An ensemble model for predicting the remaining useful performance of lithium-ion batteries[J]. Microelectronics Reliability, 2013, 53(6): 811-820. DOI:10.1016/j.microrel.2012.12.003 |
| [60] |
Li J, Stones R J, Wang G, et al. Hard drive failure prediction using decision trees[J]. Reliability Engineering & System Safety, 2017, 164: 55-65. |
| [61] |
Zhang Y Y, Li X Y, Gao L, et al. Imbalanced data fault diagnosis of rotating machinery using synthetic oversampling and feature learning[J]. Journal of Manufacturing Systems, 2018, 48: 34-50. DOI:10.1016/j.jmsy.2018.04.005 |
| [62] |
Chai Z, Zhao C. Enhanced random forest with concurrent analysis of static and dynamic nodes for industrial fault classification[J]. IEEE Transactions on Industrial Informatics, 2020, 16(1): 54-66. DOI:10.1109/TII.2019.2915559 |
| [63] |
Tang G J, Pang B, Tian T, et al. Fault diagnosis of rolling bearings based on improved fast spectral correlation and optimized random forest[J]. Applied Sciences, 2018, 8(10): 1859. DOI:10.3390/app8101859 |
| [64] |
Widodo A, Shim M C, Caesarendra W, et al. Intelligent prognostics for battery health monitoring based on sample entropy[J]. Expert Systems with Applications, 2011, 38(9): 11763-11769. DOI:10.1016/j.eswa.2011.03.063 |
| [65] |
Nieto P G, García-Gonzalo E, Lasheras F S, et al. Hybrid PSO–SVM-based method for forecasting of the remaining useful life for aircraft engines and evaluation of its reliability[J]. Reliability Engineering & System Safety, 2015, 138: 219-231. |
| [66] |
Song Y C, Liu D T, Hou Y D, et al. Satellite lithium-ion battery remaining useful life estimation with an iterative updated RVM fused with the KF algorithm[J]. Chinese Journal of Aeronautics, 2018, 31(1): 31-40. DOI:10.1016/j.cja.2017.11.010 |
| [67] |
Tian Z G. An artificial neural network method for remaining useful life prediction of equipment subject to condition monitoring[J]. Journal of Intelligent Manufacturing, 2012, 23(2): 227-237. DOI:10.1007/s10845-009-0356-9 |
| [68] |
Guo R, Li Y T, Zhao L J, et al. Remaining useful life prediction based on the Bayesian regularized radial basis function neural network for an external gear pump[J]. IEEE Access, 2020, 8: 107498-107509. DOI:10.1109/ACCESS.2020.3001013 |
| [69] |
Ren L, Sun Y Q, Cui J, et al. Bearing remaining useful life prediction based on deep autoencoder and deep neural networks[J]. Journal of Manufacturing Systems, 2018, 48: 71-77. DOI:10.1016/j.jmsy.2018.04.008 |
| [70] |
Yu W N, Kim I Y, Mechefske C. Remaining useful life estimation using a bidirectional recurrent neural network based autoencoder scheme[J]. Mechanical Systems and Signal Processing, 2019, 129: 764-780. DOI:10.1016/j.ymssp.2019.05.005 |
| [71] |
Yang B Y, Liu R N, Zio E. Remaining useful life prediction based on a double-convolutional neural network architecture[J]. IEEE Transactions on Industrial Electronics, 2019, 66(12): 9521-9530. DOI:10.1109/TIE.2019.2924605 |
| [72] |
Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386 |
| [73] |
Lu C, Wang Z, Zhou B. Intelligent fault diagnosis of rolling bearing using hierarchical convolutional network based health state classification[J]. Advanced Engineering Informatics, 2017, 32: 139-151. DOI:10.1016/j.aei.2017.02.005 |
| [74] |
Janssens O, Van De Walle R, Loccufier M, et al. Deep learning for infrared thermal image based machine health monitoring[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(1): 151-159. DOI:10.1109/TMECH.2017.2722479 |
| [75] |
邱锡鹏. 神经网络与深度学习[M]. 北京: 机械工业出版社, 2020: 109-313. (Qiu X P. Neural network and deep learning[M]. Beijing: China Machine Press, 2020: 109-313.) |
| [76] |
Guo L, Li N P, Jia F, et al. A recurrent neural network based health indicator for remaining useful life prediction of bearings[J]. Neurocomputing, 2017, 240: 98-109. DOI:10.1016/j.neucom.2017.02.045 |
| [77] |
Xia T B, Song Y, Zheng Y, et al. An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation[J]. Computers in Industry, 2020, 115: 103182. DOI:10.1016/j.compind.2019.103182 |
| [78] |
Li P H, Zhang Z J, Xiong Q Y, et al. State-of-health estimation and remaining useful life prediction for the lithium-ion battery based on a variant long short term memory neural network[J]. Journal of Power Sources, 2020, 459: 228069. DOI:10.1016/j.jpowsour.2020.228069 |
| [79] |
Ma M, Mao Z. Deep convolution-based LSTM network for remaining useful life prediction[J]. IEEE Transactions on Industrial Informatics, 2020, 17(3): 1658-1667. |
| [80] |
Chen J L, Jing H J, Chang Y H, et al. Gated recurrent unit based recurrent neural network for remaining useful life prediction of nonlinear deterioration process[J]. Reliability Engineering & System Safety, 2019, 185: 372-382. |
| [81] |
Zhao R, Wang D Z, Yan R Q, et al. Machine health monitoring using local feature-based gated recurrent unit networks[J]. IEEE Transactions on Industrial Electronics, 2017, 65(2): 1539-1548. |
| [82] |
Peng K X, Jiao R H, Dong J, et al. A deep belief network based health indicator construction and remaining useful life prediction using improved particle filter[J]. Neurocomputing, 2019, 361: 19-28. DOI:10.1016/j.neucom.2019.07.075 |
| [83] |
Wang S H, Xiang J W, Zhong Y T, et al. A data indicator-based deep belief networks to detect multiple faults in axial piston pumps[J]. Mechanical Systems and Signal Processing, 2018, 112: 154-170. DOI:10.1016/j.ymssp.2018.04.038 |
| [84] |
Voulodimos A, Doulamis N, Doulamis A, et al. Deep learning for computer vision: A brief review[J]. Computational Intelligence and Neuroscience, 2018, 2018: 7068349. |
| [85] |
Prieto J A, Rueda A, Grout I, et al. An approach to realistic fault prediction and layout design for testability in analog circuits[C]. Proceedings Design, Automation and Test in Europe. Paris: IEEE, 1998: 905-909.
|
| [86] |
Lesieutre G A, Fang L, Lee U. Hierarchical failure simulation for machinery prognostics[C]. A Critical Link: Diagnosis to Prognosis. Virginia: ASME, 1997: 103-110.
|
| [87] |
李富才, 何正嘉, 陈进. 小波域相关滤波法及其早期故障预示应用[J]. 振动工程学报, 2005, 18(2): 145-148. (Li F C, He Z J, Chen J. Wavelet transform domain correlation filter and its application in incipient fault prognosis[J]. Journal of Vibration Engineering, 2005, 18(2): 145-148. DOI:10.3969/j.issn.1004-4523.2005.02.003) |
| [88] |
顾伟, 褚建新. 基于故障统计模型的可修系统维修周期预测法[J]. 机械强度, 2000, 22(1): 1-3. (Gu W, Chu J X. Prediction method of the maintenance cycle for repairable system based on fault statistics[J]. Journal of Mechanical Strength, 2000, 22(1): 1-3. DOI:10.3321/j.issn:1001-9669.2000.01.001) |
| [89] |
Gebraeel N, Lawley M, Liu R, et al. Residual life predictions from vibration-based degradation signals: A neural network approach[J]. IEEE Transactions on Industrial Electronics, 2004, 51(3): 694-700. DOI:10.1109/TIE.2004.824875 |
| [90] |
赵洪山, 胡庆春, 李志为. 基于统计过程控制的风机齿轮箱故障预测[J]. 电力系统保护与控制, 2012, 40(13): 67-73. (Zhao H S, Hu Q C, Li Z W. Failure prediction of wind turbine gearbox based on statistical process control[J]. Power System Protection and Control, 2012, 40(13): 67-73. DOI:10.7667/j.issn.1674-3415.2012.13.012) |
| [91] |
费胜巍, 孙宇. 融合粗糙集与灰色理论的电力变压器故障预测[J]. 中国电机工程学报, 2008, 28(16): 154-160. (Fei S W, Sun Y. Fault prediction of power transformer by combination of rough sets and grey theory[J]. Proceedings of the CSEE, 2008, 28(16): 154-160. DOI:10.3321/j.issn:0258-8013.2008.16.025) |
| [92] |
曾庆虎, 邱静, 刘冠军, 等. 基于KPCA-HSMM设备退化状态识别与故障预测方法研究[J]. 仪器仪表学报, 2009, 30(7): 1341-1346. (Zeng Q H, Qing J, Liu G J, et al. Research on equipment degradation state recognition and fault prognostics method based on KPCA-hidden semi-Markov model[J]. Chinese Journal of Scientific Instrument, 2009, 30(7): 1341-1346. DOI:10.3321/j.issn:0254-3087.2009.07.001) |
| [93] |
孙博, 康锐, 谢劲松. 故障预测与健康管理系统研究和应用现状综述[J]. 系统工程与电子技术, 2007, 29(10): 1762-1767. (Sun B, Kang R, Xie J S. Research and application of the prognostic and health management system[J]. Systems Engineering and Electronics, 2007, 29(10): 1762-1767. DOI:10.3321/j.issn:1001-506x.2007.10.042) |
| [94] |
Huang R Q, Xi L F, Li X L, et al. Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods[J]. Mechanical Systems and Signal Processing, 2007, 21(1): 193-207. DOI:10.1016/j.ymssp.2005.11.008 |
| [95] |
孙强, 岳继光. 基于不确定性的故障预测方法综述[J]. 控制与决策, 2014, 29(5): 769-778. (Sun Q, Yue J G. Review on fault prognostic methods based on uncertainty[J]. Control and Decision, 2014, 29(5): 769-778.) |
| [96] |
年夫顺. 关于故障预测与健康管理技术的几点认识[J]. 仪器仪表学报, 2018, 39(8): 1-14. (Nian F S. Viewpoints about the prognostic and health management[J]. Chinese Journal of Scientific Instrument, 2018, 39(8): 1-14.) |
| [97] |
Khan S, Yairi T. A review on the application of deep learning in system health management[J]. Mechanical Systems and Signal Processing, 2018, 107: 241-265. DOI:10.1016/j.ymssp.2017.11.024 |
| [98] |
Wang B, Lei Y G, Li N P, et al. Deep separable convolutional network for remaining useful life prediction of machinery[J]. Mechanical Systems and Signal Processing, 2019, 134: 106330. DOI:10.1016/j.ymssp.2019.106330 |
| [99] |
Shao H D, Xia M, Han G J, et al. Intelligent fault diagnosis of rotor-bearing system under varying working conditions with modified transfer CNN and thermal images[J]. IEEE Transactions on Industrial Informatics, 2021, 17(5): 3488-3496. DOI:10.1109/TII.2020.3005965 |
| [100] |
Booyse W, Wilke D N, Heyns S. Deep digital twins for detection, diagnostics and prognostics[J]. Mechanical Systems and Signal Processing, 2020, 140: 106612. DOI:10.1016/j.ymssp.2019.106612 |
 2022, Vol. 37
2022, Vol. 37
